Tessellation Artwork  Bravo to all of the students who worked on their tessellation art and brought something in for the class to see! It was wonderful to observe the variety of visual ideas students have developed in these early efforts. Students should continue to work at home on creating their own unique tessellation patterns from regular polygons, using the translation method we learned in class last week. Try using rotation and reflection in your designs, and don't be afraid to experiment with color, or perhaps combinations of polygons. The possibilities are truly as unlimited as your own imagination! The Intrigue of Pascal's Triangle 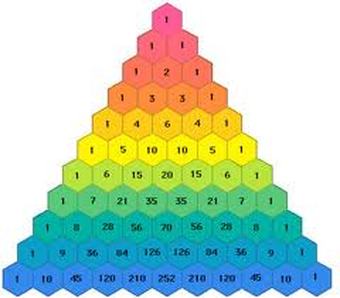 This week in class we took an introductory look at the seemingly simple yet powerful triangular arrangement of numbers known as Pascal's Triangle. While Blaise Pascal, a 17th century mathematician, is credited for developing many of the properties and applications of the triangle, this amazing combination of numbers was actually known independently by both the Persians and the Chinese as early as the 11th century. We covered a lot of material in class this week and most of it was new to the students. I provided them with a handout of information summarizing what was discussed in class (also found HERE). I strongly encourage all students to carefully review this material again as part of their homework. Class Review... We discussed how to create the triangle (each number is the sum of the two numbers above it) and spent time looking at some of the interesting hidden patterns within it:
If, for instance, you pick any two of five items, the number of possible combinations is 10, found by looking in the second place of the fifth row (not counting the 1's). We worked out a similar problem in class, first using inductive reasoning, and listing all possible unique combinations. Then, we looked at how easily we can apply Pascal's Triangle to solve the same problem. This can be worked out mathematically using a simple formula, referred to as "n choose k" where n = the number of total items and k = number of items chosen. So, for the example above, n = 5 (5th row) and k = 2 (2nd place in the row), which yields the answer 10 from the triangle. And Homework... As part of this week's homework, students will solve several of these types of problems. Additionally, I would like them to express their answers using the entire mathematical formula, including the factorial math: This can be very useful because now you can work out any value in Pascal's Triangle directly, without constructing the whole triangle! Fun with Pentominoes Finally, we wound down our class this week with some relaxing (or was it frustrating?!) hands-on geometry time using pentominoes. Students were challenged to make rectangles out of pentominoes (five equal squares that share at least one side, with no windows) and solve various puzzles from a worksheet. These were much more challenging than they initially seemed! If you would like to continue working on these types of puzzles at home, you can try "virtual" pentominoes HERE.
Enjoy! Comments are closed.
|
Categories
All
Archives
May 2016
|

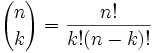


 RSS Feed
RSS Feed