with Kim Rodgers

We warmed up the class by discussing strategies for solving 33 x 5. We came up with three ways to arrive at the same answer using different processes. One of the strategies involved multiplying 33 by 10, since 10 is an easy number to multiply by, and cutting the answer in half. Another student mentioned that this might not be a good strategy to use if we were multiplying by 4, which led into a discussion about using strategies in our Algebra Tool Kit. We don’t use all of the strategies all of the time -- we find the ones that suit the problem.

We moved on to reviewing what we had worked on in class the previous week with our Morph Machine, catching up a couple of students who had been absent. Going Backwards was added as a strategy to solving a problem using inverse operations. After performing some steps together on several examples, the students began to understand the value of this strategy. Because this may be a new concept for many students, I am providing a more detailed description of Monday's class in case any of our families would like to review the material at home. Here’s what we worked on in our Morph Machine: 

Students picked a number between 1-20 for n and wrote it in their journals. They then took that number through a series of operations.

n=                _____
Add 1             +1
Multiply by 3   x3 
Add 4             +4 
Subtract 7       -7 
Morphed n = _____

Once they morphed their numbers, volunteers were called on to share them. Together as a class we used 3 of these morphed numbers to work our way backwards to find the original numbers. For instance, if the morphed number was 6, we worked backwards using inverse operations like these: 

Morphed n =     6
Add 7              +7 
Subtract 4        -4 
Divide by 3       /3 
Subtract 1        -1 
n=                     2

Here’s where the tricky part came in. We discussed how variables can define a rule for each step so that any number n will work. So, using 6 as the morphed number, we look at the first step to work backwards -- subtract 7. We know the answer is going to be 6, so we set it up like this:

n - 7 = 6



What is the inverse operation of subtracting 7? Adding 7! So we must do that, but we must do that to both sides:

n - 7 + 7 = 6 + 7
n + 0 = 13
n = 13

Taking 13, we move one more step backwards to add 4.

n + 4 = 13

What is the inverse of adding 4? Subtracting 4! So we must do that, but we must do that to both sides:

n + 4 - 4 = 13 - 4 
n + 0 = 9
n = 9 

We continued doing this together as a class until we got back to our original number, n. I then had them pair-up to further practice these problems. Many were still stumped. As I made my way around the room giving hints and advice, some students began to have a glimmer of understanding. As soon as I saw that, I had those students help others who were having trouble. Time went so quickly! As class ended, I told them that we would be working on this again next week, and if they felt like they still didn’t understand, that was okay. It’s a difficult concept to grasp. I will be presenting the same concept next week using a scale as a visual -- to drive home the point that both sides of the equation need to be balanced. Whatever happens to one side has to happen to the other!

I’m not a big fan of computer games, but I do have one to recommend from Mrs. Yoder who teaches Computer Science at Mosaic. It secretly teaches kids Algebra, but don’t tell them that! It’s called DragonBox. There are two versions. If Algebra is a new concept for your child I would start with the beginner version. If your child has had some practice with it you might want to check out the 12+ version. It really drives home the point that whatever is done to one side of the equation has to happen to the other side, as well.

See you next week! 

with Leigh Ann Yoder

We opened class with a review of our homework. The students discovered that human error plays a role when it comes to coding and decoding a Huffman Code message, but hopefully can appreciate that computers don't make nearly as many errors. The students did excellent work on their Decision Trees from last week, and we quickly went over a bottom-up method of designing the tree. Lastly, I was pleased that most of the students were able to develop an algorithm for solving the Master Mind game played for homework.

We discussed a theory by Claude Shannon (first, we defined theory), which states that a message cannot be compressed less than its entropy. The students were taught the meaning of entropy and how to calculate it. They will be working on this for homework. The entire class will be testing Shannon’s theory that the entropy of text messages is, on average, 1.6. This simply means that it takes 1.6 guesses (on average) to guess each letter of a message.

Most of our class time was focused on introducing our new unit. Now that the students have a firm fundamental understanding of data representation, it is time to move on. In the next few weeks, we will focus on putting computers to work. Specifically, how we can access, store, and manipulate data efficiently for our benefit.

I introduced the terms, Procedure, Sort, and Search as they pertain to Computer Science. These terms will continue to be reviewed and by the end of our unit the students will be confident of their meanings and applications. I also gave a very brief history lesson on the origins of the word algorithm. The word is related to the works of Muḥammad ibn Mūsā al-Khwārizmī, a mathematician who joined an academic center known as the House of Wisdom in Baghdad around 800 AD. He is also considered the father of Algebra.

Computers are often required to find information in large collections of data, which require quick and efficient methods. Using a simple Battleship-type game, the class is experimenting with different searching algorithms. Today we used Linear Searching to locate our partner’s ships. Students quickly identified the inefficiency of Linear Searching. Next week, we will play two more Battleship games, which will demonstrate more efficient searching methods.

with Michelle Cameron

We had a great class on this last October meeting of the year…

Among the comments on today’s sampling of writing were: 

• Dialogue punctuation and paragraphing – this is still an area that needs work. That’s not a surprise – a lot of the adult writers I work with don’t get it either. We’ll keep focusing on this. 
  
• Among the important aspects of dialogue is to make sure each character sounds true to him or herself. 
  
• We talked a little about “suspending disbelief” – making the unreal in a story seem real to the reader by being true to the internal rules of the story. 

• A beautiful autumn poem elicited the following comments: 
  

              - Poetry is condensed meaning and feeling.
              - Poems don’t need to rhyme! But they do need to adhere to an internal rhythm.
              - Poems don’t need to follow the same rules of punctuation or capitalization as prose.
              - This particular poem used the senses beautifully (previewing our topic for next week!) 

We did another “pick three” exercise today, picking three “spooky” words out of my magician’s hat – just in time for Halloween!

The stories that came out of this exercise ranged from spooky to violent, foreboding to unexpected.

As we had a few minutes to spare when the kids were done, we took what they considered their favorite line out of each story and put them together into one fairly nonsensical story. I’ve rearranged the sentences to make the most sense out of what they gave me:

“Why hello, child, do you need a ride home?” The Wizard’s name was Drake the Doofus. His whole figure appeared as if it would melt into the night.

The ominous crooked mansion stands proudly at the top of the mountain. I saw a rainbow in the distance.

I howled as they hacked off my finger with a kitchen knife. 

Uncle Vicky, married to Aunt Icky, got me a spelling book of how to spell spells.  I just tried to turn them out.

Well, I did say it was fairly nonsensical!

As usual, one of three choices:

• Complete what they started in class.
  
• Work on something they started previously.
  
• Write something completely new!
  

Happy Halloween, everyone!

with Kim Rodgers

The Morph Machine was introduced in class on Monday!

This machine has two chambers. The first transforms the number going into the machine, while the second restores the number back to its original number through different processes. 

Mental math was used to take each student’s choice of a number through the first stage of the Morph Machine. Once students' numbers were sufficiently morphed using several steps, we made a T-table and they shared their outcomes. I surprised them all by “guessing” their restored number quickly and correctly! Once we did a handful of these morphed/restored numbers the students began to see a pattern and could “guess” the restored numbers, as well. Even though there were several steps to get to the morphed number, they saw that they could do one step to get back to their original number. We did several of these together, with the students seeing patterns more quickly each time.

In order to take a mental break, the students worked on number tile problems with a partner. You should have received an e-mail with a photo of the one they were working on. Some of the students wanted to work on the solutions at home. After about 15 minutes we went back to the Morph Machine.

We thought everyone would like to see some images from our Afternoon Enrichment session this week. The theme was Dynamic Crafts and the students made:

• Rubber Band Bracelets
  
• Marionettes
  
• String Art
  
• Friendship Bracelets
  
• Origami
  
• Bead Designs 

Fun times!

We read Story of the World (Volume 1) Chapter 3 in our morning class and learned about two of the earliest forms of writing - cuneiform and hieroglyphics.  

Students had the opportunity to write their names (or create secret messages) in the ancient Sumerian language of cuneiform, using soft clay and sculpting tools.  Once they were satisfied with their clay "tablets", we moved on to translating our names into hieroglyphs, the symbols used by ancient Egyptian scribes.  We wrote our names on paper, but discussed the fact that ancient Egyptians initially carved hieroglyphs into heavy stone tablets until they invented a method for creating paper from papyrus.  I think we all agreed that writing in hieroglyphics was harder than cuneiform because many of the symbols are quite complex!  

The students can continue writing more messages at home in both cuneiform and hieroglyphics using the handouts I sent home with them.  Not only does this activity practice fine motor skills (especially using the clay); it also challenges them to be patient in creating each character, and to think about how to spell words. 

Students also played bingo using words from our Word Wall and other vocabulary we have learned studying ancient Egypt.  While most of the students cannot yet read or spell many of these words, just listening for beginning sounds and searching for correct letters provides good practice for early reading and sight word recognition.  

Additionally, it prompted the students to work collaboratively and to help each other succeed, which is always a joy to facilitate! 

This week in our afternoon class we connected our previous study of the solar system and the Nile River to the calendar. We learned about the three seasons of the ancient Egyptian calendar, and compared it to our calendar. 

After our lesson the children were free to work on several different activities.

with Michelle Cameron

After our revision session last time we met, I edited the revised pieces. I told them that I’m approaching their work as an editor. 

In case anyone wants to conference with me on their work, I plan to arrive a half hour early to talk to them. Please encourage your writers to take advantage of this.

We talked about some common issues I’m seeing:

• Overwriting – I’m encouraging them to write simply and directly, and suggested that they read their work aloud every time.

• Unnecessary transitions – particularly if the piece is told chronologically. One unnecessary word many of them are using is the word “then.” 

I’m delighted to see longer pieces from many of the writers – and if the pieces aren’t longer, they’re bringing more of them in. Some of the aspects of writing we discussed were:

• Flash fiction – these are becoming popular, but they still need to:

              - Have a beginning, middle and end
              - Be a satisfying store, which can mean more backstory, description and emotion

• How prologues are used in books they’ve read: 

              -  How some readers don’t read them, so they can’t contain necessary information
              -  How some authors craft them so that you forget them until the end of the book

• How effective body language can be when used properly.

• How appropriate dialogue can add to a story’s flavor and characterization (we’ll talk more about dialogue in a bit). 

• Keeping minor characters consistent in short stories (though they can grow and change in novels) 

• Setting up a situation in a story to lead (or mislead) the reader

• How to work with magical properties in a story. The fact that magic is employed doesn’t mean the reader doesn’t need to know its inner workings. 

We then talked about dialogue, including:

• The grammar of dialogue: 

            -  When to use a comma and when a period
            -  Paragraphing

• Making sure the reader always knows who is talking
  
• The fact that dialogue doesn’t happen in a vacuum, that setting and movement are necessary.
  
• The fact that “said” is perfectly acceptable and should be used rather than alternate terms such as “exclaimed,” “retorted,” etc. 
  
• The fact that sentence tags (said, asked, yelled, etc.)  can and should be dropped if it’s clear who is speaking.
  
• That using a character’s body language is often a better thing to use than sentence tags.
  
• That they should avoid adverbs (not always, but mostly).
  

They then split into partners to work on a scenario, employing dialogue. 

As always, they have a choice:

• Continue something they’ve already begun. 
  
• Continue the dialogue they started in class – they can work with their partner or simply continue on their own (and they’re allowed to change it as they’d like)
  
• Start something new.

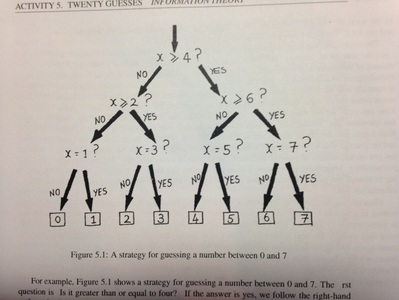
with Leigh Ann Yoder

The first half of our class this week was spent learning a method of text compression referred to as Huffman Code. The Huffman Code offers a solution to representing text while minimizing the number of bits used. One of the main purposes was to introduce the concept of a Decision Tree, which was defined in class. I want the students to gain confidence working with Decision Trees as we enter our second unit. They began working on their own Trees in class and have been asked to complete them for homework.

The second half of the class was devoted to our new topic called: Information Theory, although the students will not yet recognize that terminology. We are working through a set of familiar activities to help us quantify how much information something has. We used games similar to Twenty Questions and Hangman. I am trying to lead them to quantify an abstract concept. This is not an easy lesson, even for adults. We worked slowly through several scenarios, and will continue with more difficult ones next week.