Development and Use of Math  This week in class we reviewed what we have discovered so far on our journey through history about how ancient civilizations used and developed math. We discussed the Babylonians practical use of accounting tokens for trading goods, keeping records and dividing up land; and the Egyptians use of geometry and measurement for building amazing works of architecture such as pyramids and temples. We acknowledged the intellectual leap from simple counting with tally marks to the use of a mathematical symbols (arabic numbers) as a further level of abstraction and a universal way to assess quantity and perform calculations. The fact that the symbol '5' could stand for number of sheep as well as number of people or sacks of grain provided a language for mathematical dialogue. It was the Greeks however who really pushed math to a whole new level by marrying it with science. In fact, they saw math as the language of science, not just a practical endeavor, but a way to reason and understand the world. 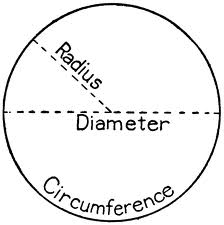 We reviewed the parts of a circle using the Student Quest worksheet which was due as homework and then students spent some time measuring a variety of circular objects of different sizes using string and recording the circumferences (C) and diameters (D). We then computed the value of C/D for all objects to see that the value of this ratio, regardless of circle size, is nearly the same (allowing for measurement differences). The ancient Greeks, along with many other ancient cultures, had observed the same thing. The ancients were fascinated with the perfect form and function of the circle and many ancient mathematicians tried to determine the exact mathematical expression for this ratio. Why? Because if determined it would allow them to accurately compute the circumference of a circle (and it's area), and make it easy to measure circles of all sizes! Of course we now know this number as pi (the 16th Greek letter). We discussed why there was such difficulty in determining the value of pi. Turns out, it's a complicated number! And that is something that did not sit well with the Greeks who valued form and order and exactness in their math. Pi in fact is an irrational number - meaning the digits beyond the decimal point do not repeat in a regular pattern. Mathematicians now believe we will never find its exact value, as no current computing technology has determined an end point to the number pi. We briefly looked at how Aristotle attempted to determine the value for pi by "squaring the circle". I would encourage students to carefully read about this method in their Student Quest Guides (pages 25-26) to understand how he was able to arrive at his "magic number". At the conclusion of our class we touched on some of the ideas and work of Pythagoras, possibly the most famous Greek mathematician. He believed that the universe could be best understood through mathematics and in fact that all parts of the universe interact like instruments in an orchestra. We will continue our discussion of Pythagoras, his society, and the development of the Pythagorean Theorem next week. We will also look at the work of Democritus and his thoughts on the basic building blocks of life - the atom. Homework Students should read Chapters 10 & 11 in preparation for our class next week. I have also asked students to write a one-paragraph response to the following question (which will require both research and thought):
Comments are closed.
|
Categories
All
Archives
May 2016
|

 RSS Feed
RSS Feed