On 10/22, we tackled several Distribution Dilemmas. These are problems that require the student to think beyond the boundaries suggested by the problem, to reach a not-so-obvious solution. Specifically, we looked at a couple of inheritance puzzles which required the use of unit fraction proportions to determine how to divvy up sheep left by a shepherd to his children. It was a good review of basic fraction calculations for most students, and pushed them to think of a creative way to resolve the dilemma of having proportions that do not add up.  We then played an Iterated Sharing game, involving....Candy! Everyone sat in a circle and candy was distributed randomly to each person, though all were given an even number of pieces. A reserve supply was placed in the middle of the circle. At each iteration, students gave half their candy to the person on their left, and recieved a supply of candy from the person on their right. We then recounted our individual totals. If you had an odd number, you take a piece from the reserve supply to boost your pile back up to even, and everyone iterates again. I asked students to contemplate what would happen if we continue to perform this maneuver again and again. Will everyone's supply grow without bound? Will the distribution stabilize at some point? Will any pattern emerge? Is it possible to even predict the result? Interestingly, most students initially thought their piles would grow unbounded (or perhaps that was wishful thinking!). However, once we stepped through a few iterations, it started to look like the piles were beginning to even out, and students changed their predictions. At the beginning of the game, we noted the students with the largest and the smallest number of pieces before any iterated sharing began. At the conclusion of the game, everyone had the same number of pieces and we discussed how we can determine an upper and lower bound on the amount of candy simply by noting the largest and least initial amount received. The fact that we continued to halve, pass, and then even out our piles forces the distribution to stabilize. No matter what the initial distribution of candy or how many people are in the circle, the distribution will eventually equalize. This exercise was a great introduction to the basic concepts of computer simulation and modeling. And, as luck would have it, a hurricane called Sandy was brewing out in the Atlantic, and soon would provide a real-life example of just how important simulation and prediction can be! On 11/12 we met after two weeks of cancelled classes due to the hurricane aftermath. I took the opportunity to explain the basics of hurricane prediction and the use of 3-D global and regional climate simulation models. The basic iterated sharing game with candy had laid some groundwork for understanding how scientists develop and run simulations to model highly complex physical processes, such as weather. We also began work on our on-going class project affectionately known as, The Popcorn Problem. I have split the class into two teams and challenged each to determine how much popcorn it would take to completely fill our classroom. For the past few weeks students have been measuring the classroom dimensions, estimating the size of popcorn, and developing a plan for determining their solution. More to come on this strange and tasty endeavor! 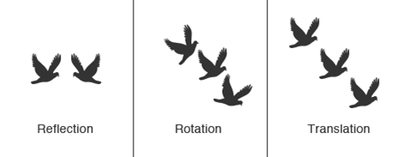 For our class on 11/19, we shifted gears to focus on concepts of geometry and Symmetry. We looked at imagery of all the myriad places we find symmetry in our world - art, architecture, nature (animals, plants), music, dance, etc. and learned about the three main types of symmetry - reflection (mirror), rotational, and translation. Students then worked problems to find all the lines of symmetry in regular and irregular polygons, played around with decoding messages in mirrored text and worked on creating their own mirrored codes. The most challenging work was sent home with them - finding congruent halves in shapes that contain a combination of reflection, rotation, and translation symmetry. Students must be able to visually see how to flip, turn, and/or slide one figure so that it fits exactly onto the other congruent half in order to solve these problems. We will continue our look at geometric properties in our next few classes as we discuss tessellations and fractals. Comments are closed.
|
Categories
All
Archives
May 2016
|


 RSS Feed
RSS Feed