|
with Kim Rodgers Distributive Property for Addition/Subtraction For the last couple of weeks we have been working on the distributive property for addition which is stated as: a (b + c) = (a x b) + (a x c) We started by using actual number problems to prove how this property works before introducing the property algebraically. After using base ten blocks the first week, we worked on problems in our notebooks last week. Those who finished all the problems began helping their classmates. The students took turns “teaching” the class how they solved each problem. We then moved on, trying to express the problems we had been working on in an algebraic way. We took the problem 3 x 46. After splitting 46 into tens and ones (40 + 6), we assigned a letter to each number in the problem: 3 x (40 + 6) = (3 x 40) + (3 x 6) a = 3 b = 40 c = 6  This led us into the property itself, which we added onto our Algebra Toolkit. We discussed why it might be called the distributive property, with a consensus that “a” has to be distributed to “b” and “c”. This week we took what we learned about the distributive property for addition and asked if we could do the same thing using subtraction. We took one problem we had worked with when using addition (6 x 39) and asked how we could express 39 as a difference of two numbers instead of an addition. We worked through it like this:  After doing one more together we mapped out the steps and the students tackled more problems on their own. I really saw a difference from the week before. They had the concept of distribution down. The only problem was they kept reverting back to addition. We laughed as it kept happening over and over, which led us into a great discussion about why it’s good to SHOW YOUR WORK! I have been emphasizing this over the last several weeks because it’s very difficult to see where the problem lies if all you have is an answer. Because they were showing their work I could see where they were having problems, and most of the time it was a mistake that had nothing to do with the concept of the distributive property. They added instead of subtracted or they wrote a number down wrong, etc. It was clear to them by the end of class yesterday that it only helps them when they show their work. Wrapping up our work on the distributive property for subtraction, we expressed it algebraically and put it on our toolkit as well: a (b - c) = (a x b) - (a x c) Next week we will begin discussing how algebra is used in the real world. They are welcome to do some research in this area by looking into how people might use algebra in their jobs. They began discussing this a little bit at the end of class and seemed excited by it. Looking forward to seeing what they come up with! Comments are closed.
|
Categories
All
Archives
May 2016
|

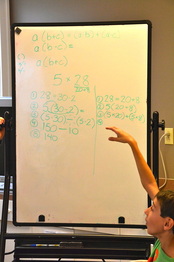
 RSS Feed
RSS Feed